これはクリス・マーテンソンさんの講義「Crash Course(2014年版)」を安納献さんが翻訳したものです。
※ 経緯はこちら [クラッシュコース日本語訳を、安納献さんの翻訳で公開&アーカイブします]
※ 本文内の太字は、編集・校正をしたテンダーによる可読性を上げるためのもの
クラッシュコースでは、いくつかの基本的な重要な概念を学びます。
その中でも特に重要なのは指数関数的成長です。
指数関数的成長を理解することで、より良い未来を作る可能性が大きく向上します。
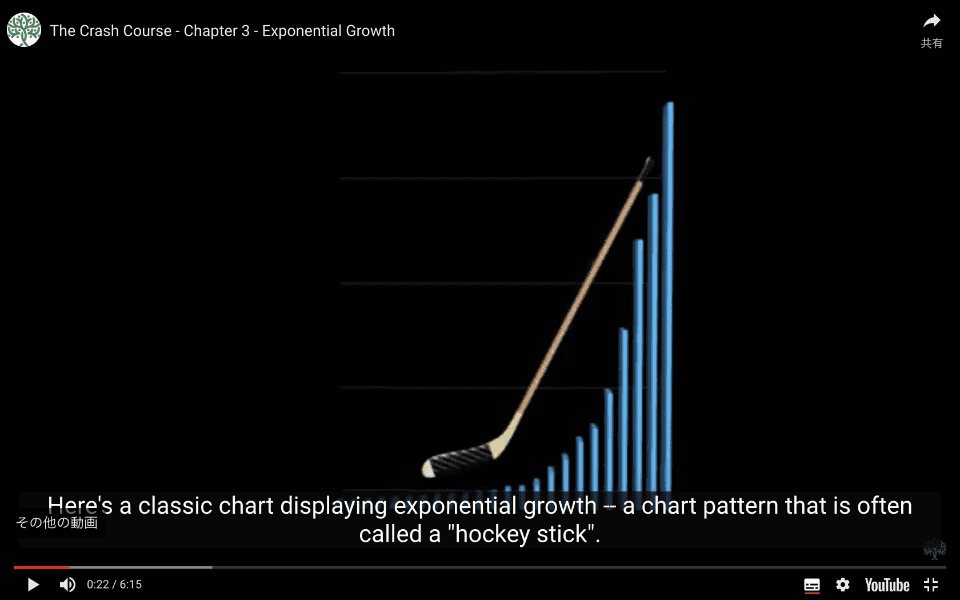
これが指数関数的成長を示すクラシックなチャートであり、しばしばホッケースティックと呼ばれるパターンです。
ここでは、時間の経過とともにある量をグラフにプロットしています。
このグラフがこのような形になる唯一の要件は、測定対象が各時間単位ごとに一定の割合で成長することです。
成長率が遅いほど、このホッケースティックの形を視覚的に確認するためには長い時間が必要です。
このグラフからもう一つ知っていただきたいのは、指数関数がある一線を超えると、成長「率」が一定であっても、そして非常に低いままであっても、増減する実際の「量」は一定ではないということです。
量はますます多く積み重なります。
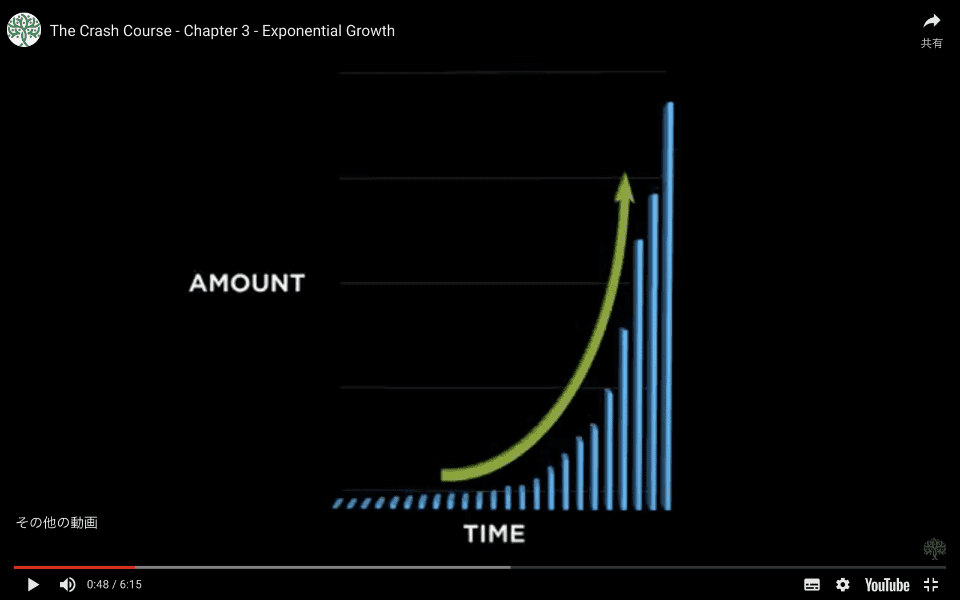
この具体的な例では、年間成長率が1%未満であった何かのチャートを見ています。
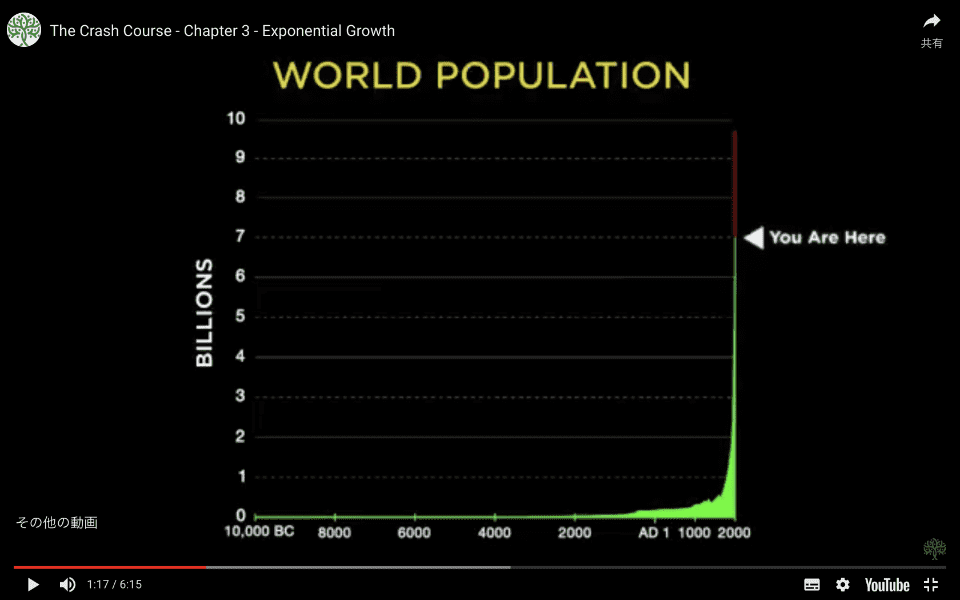
これは世界人口であり、年間約1%の成長率であるため、このホッケースティックの形を検出するには数千年を見る必要があります。
緑色は過去のデータであり、赤色は2050年までの国連の最新の人口増加予測です。
確かに、数学に詳しい方々は、私がこの情報を正しく提示していないことを心地悪く感じ始めるかもしれません。
数学者は指数関数的成長を変化率の観点から定義するように訓練されていますが、私たちは変化量に焦点を当てます。
どちらも有効ですが、数式として表現するのが簡単な方法と、ほとんどの人が直感的に理解しやすい方法があるだけです。
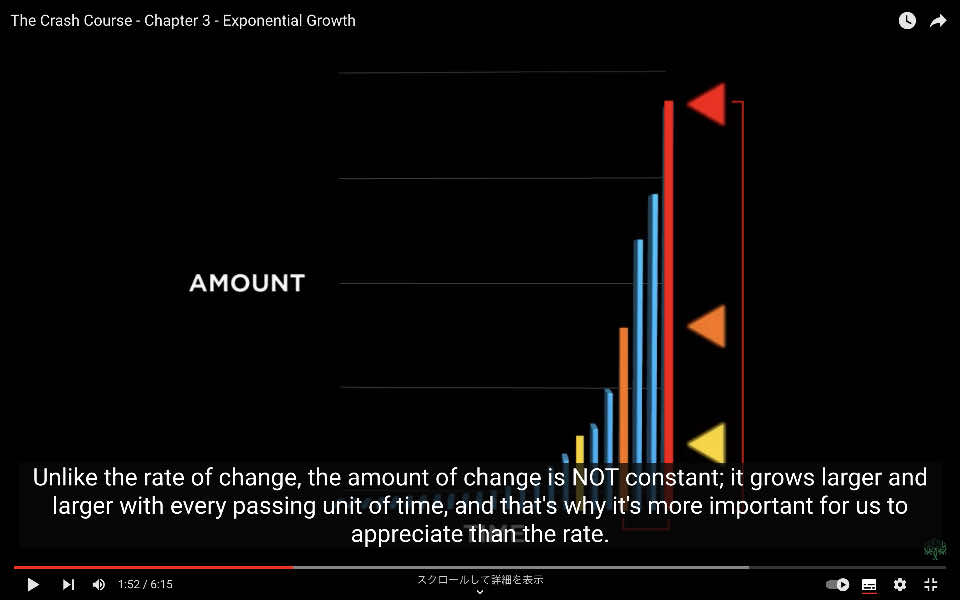
変化率とは異なり、変化量は一定ではありません。
時間が経過するごとに大きくなり、それが私たちにとって理解する上でより重要なのです。
この概念は非常に重要なので、次の章を使ってこれを説明します。
また、数学者は指数関数のグラフにある一線はないと言います、なぜならばこれは左側のスケールをどこに描くかの問題に過ぎませんから。
つまり、左側の軸を適切に調整すれば、指数関数のグラフは常にホッケースティックのように見えます。
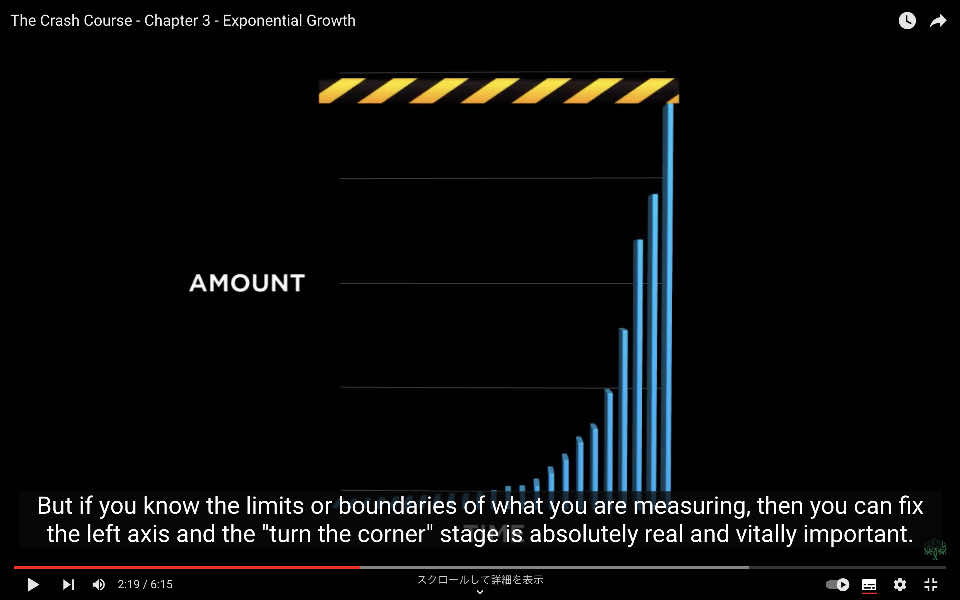
しかし、測定対象の限界や境界を知っていれば、左側の軸を固定することができ、ある一線は絶対に実在し、非常に重要です。
この違いは重要であり、私たちの未来はこれを理解することにかかっています。
例えば、地球の人間の総収容能力は数十億の増減はあるにせよ、この範囲内にあると考えられています。
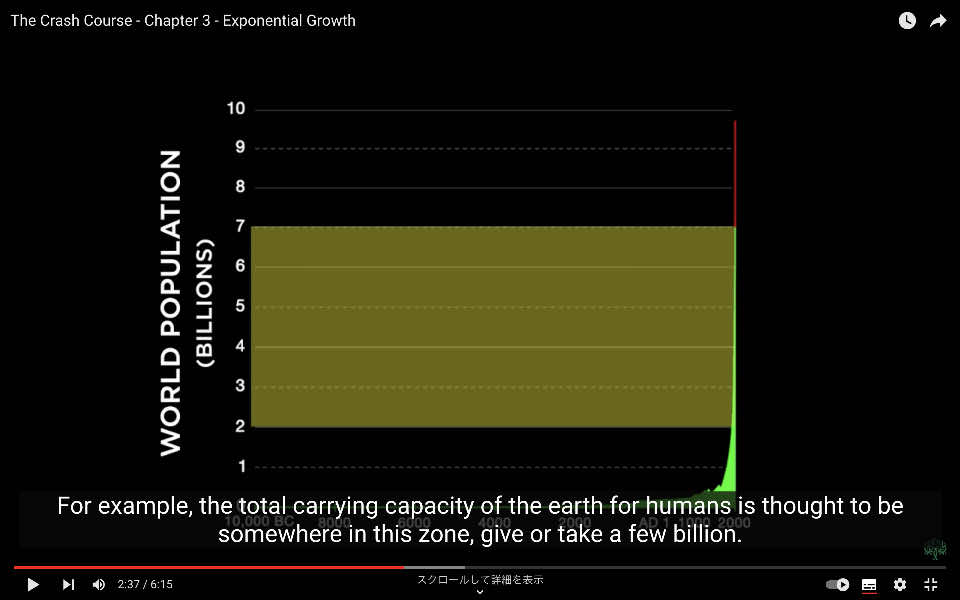
このため、ある一線は非常に現実的で、私たちにとって重要であり、グラフのトリックではありません。
指数関数の重要なポイントは、皆さんに是非とも覚えていてほしいことは、加速の概念に関連しています。
指数関数的成長の重要な特徴を、時間の単位ごとに増加する量が大きくなることとして考えるか、追加される量の単位ごとに時間が短縮することとして考えることができます。
どちらにしてもテーマは加速です。
人口を例にとると、地球上に100万人の人々がいる状態から始め、成長率を年間わずか1%に設定した場合、
- 10億人に達するまでに694年かかりますが、次の10億人にはわずか100年しかかかりません。
その後、
- 次の10億人には41年
- 次には29年
- 次には22年
- 次には18年
- そして最後の10億人にはわずか15年しかかからず、
- 結果的に70億人に達します。
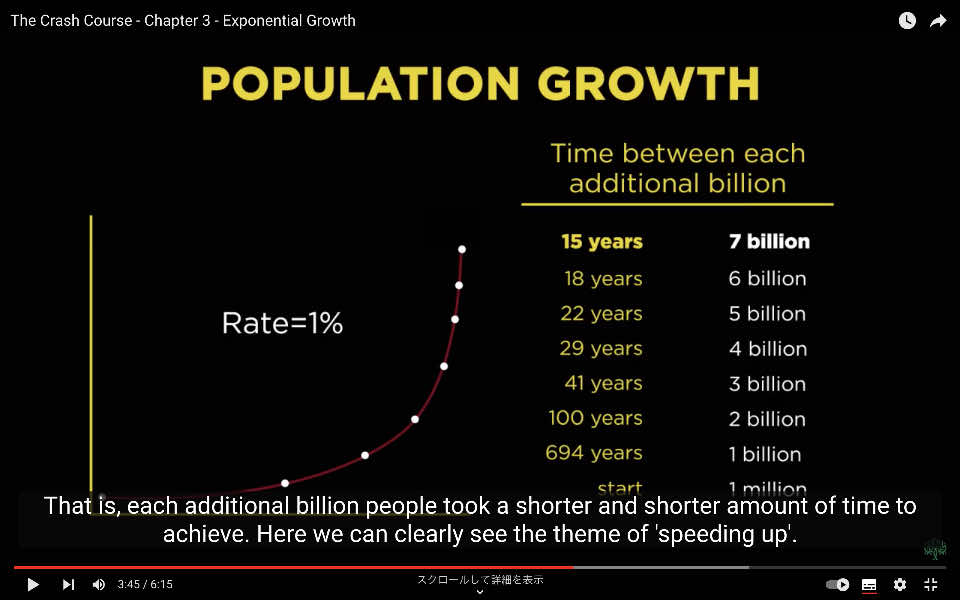
つまり、各追加の10億人にはより短い時間しかかかりませんでした。
ここで、加速のテーマが明確に見られます。
次のチャートは、石油の世界的な消費量です。おそらく最も重要な資源であり、年間約3%の速い成長率で成長しています。
過去150年間、石油で経済を動かし始めてから、このホッケースティックの形を簡単に検出できます。
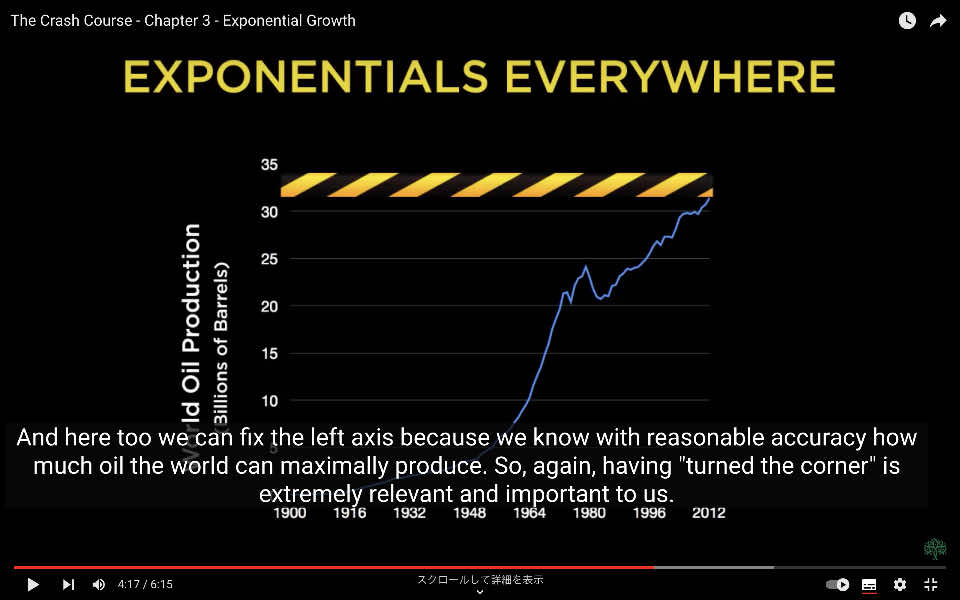
ここでも、世界が最大限に生産できる石油量を合理的に正確に知っているので、左側の軸を固定することができます。
したがって、ある一線は私たちにとって非常に重要であり関係があります。
そして、これは米国の貨幣供給量です。年間5%から18%もの驚異的な成長率で増加しています。
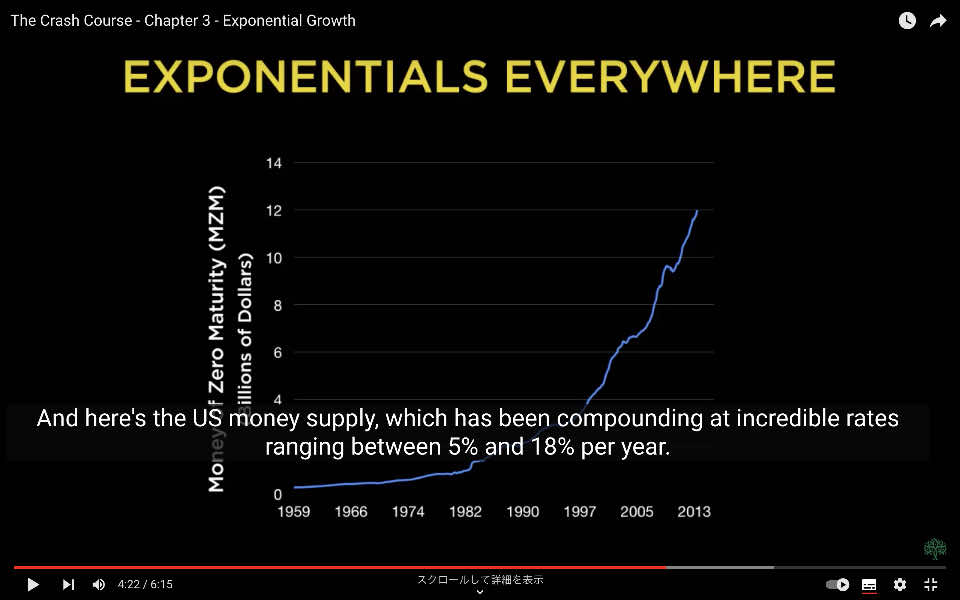
したがって、このチャートではホッケースティックの効果を確認するために数十年しか必要ありません。
これらは世界中の水の使用量、種の絶滅、乱獲された漁業、失われた森林被覆です。
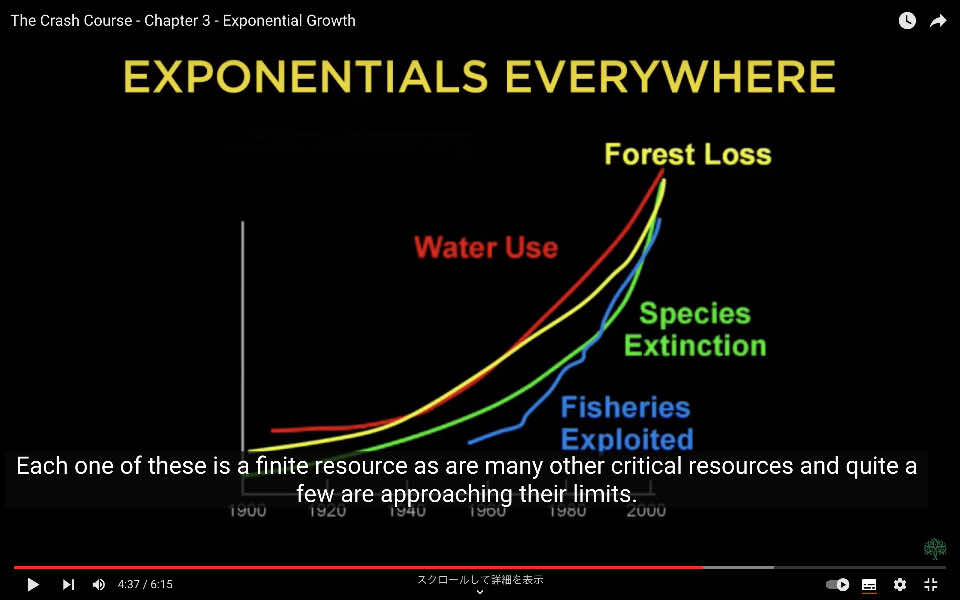
これらのそれぞれが重要な資源であり、多くの他の資源も同様に、かなりの数がその限界に近づいています。
これが私たちが住んでいる世界です。
変化のペースが加速しているように感じるなら、それはその通りだからです。
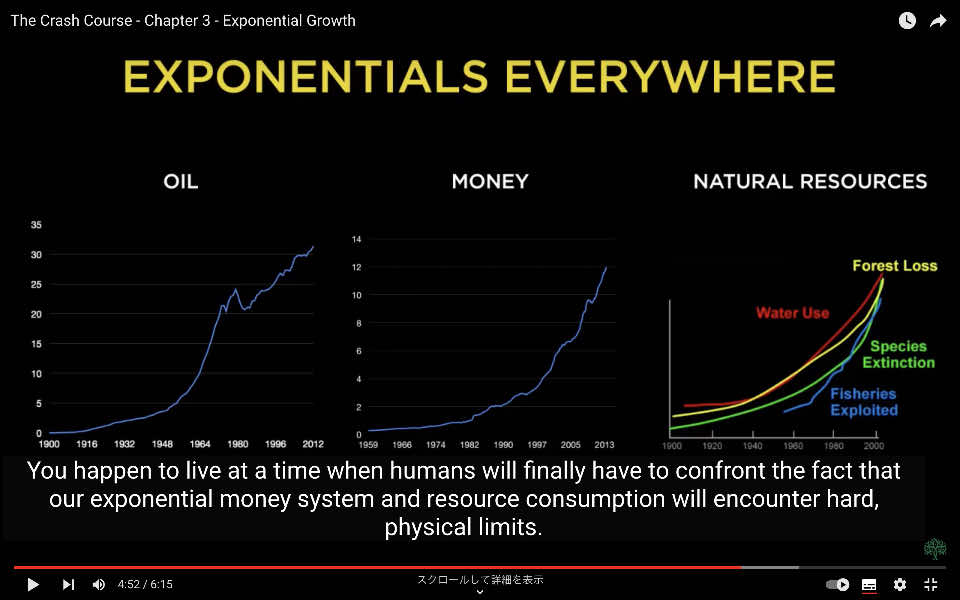
あなたは、指数関数的な貨幣システムと資源消費が物理的な限界に直面する時代に生きているのです。
そして、これらすべての背後には、地球に住む人々の数が引き続き指数関数的に増加し、加速しているという事実があります。
これらのチャートのそれぞれを一つずつ取り上げると、地球上のすべての真摯な人々の十分な注意を引きつけるられるはずです。
しかし、私たちはそれらが実際にはすべて関連し、つながっていることを理解する必要があります。
それらはすべて複合的なグラフであり、複合的な力によって動かされています。
一つの問題を解決しようとする場合、その問題が他の問題とどのように関連しているかを理解する必要があります。ここに表示されていない多くの他の問題とも関連しています。
あなたがここで、この歴史の瞬間に、貨幣から人口、種の絶滅に至るまでのすべてに関連する複数の指数関数的なグラフの存在下に生きているという事実は、あなたの人生とあなたに続く人々の人生に強力な影響を及ぼします。
これは、あなたが最も注意を払うのに値するものです。
これらのグラフを少しでもよく理解するための例に進みましょう。
次の章「複利が問題」にお付き合いください。

クラッシュコース 全容
– なぜ、クラッシュコースを日本語に翻訳して公開しようと思ったか?
はじめに
第1章 – 3つの信念
第2章 – 3つのE
第3章 – 指数関数的成長
第4章 – 複利が問題
第5章 – 成長 vs 繁栄
第6章 – お金とは何か?
第7章 – お金の創造:銀行
第8章 – お金の創造:連邦準備銀行
第9章 – アメリカのお金の短い歴史
第10章 – 量的緩和 (QE)
第11章 – インフレ
第12章 – 1兆ドルってどれくらい?
第13章 – 借金
第14章 – 資産と負債
第15章 – 人口動態
第16章 – 貯蓄と投資の国家的な失敗
第17章 – 資産バブルを理解する
第18章 – 曖昧な数字
第19章 – エネルギー経済
第20章 – ピーク・チープ・オイル(安価な石油のピーク)
第21章 – シェールオイル
第22章 – エネルギーと経済
第23章 – 環境 – 枯渇する資源
第24章 – 環境 – 増加する廃棄物
第25章 – 未来の衝撃
第26章 – 私は何をすべきか?









コメント